By , , femtoG AG, and , Cambustion Ltd.
We present a novel approach that introduces mass as a fundamental metric for characterizing the size and structure of pigments and nanoparticles. This offers the potential to establish a new standard for particle size determination. Leveraging measurement techniques developed in aerosol sciences, we apply them to uniquely analyze pigment particles in an application-oriented manner.
Engineered nanomaterials are produced at a massive scale, ranging from 103 to 107 tons per year. The physical properties of individual particles, aggregates, fibers, etc., profoundly influence the application performance of these materials. Traditional methods for characterizing physical dimensions are either expensive and time-consuming (e.g., TEM imaging) or limited to equivalent diameters. For instance, laser diffraction size analysis requires the refractive indices for a wide range of color pigments and struggles to accurately measure nonspherical or aggregated particles.
Moreover, various material properties are mass-based metrics, facilitating the calculation of other essential values. For instance, using skeletal density (g/cm3) or specific surface area (m2/g), one can derive absolute particle volume or surface area and key performance indicators like the number of particles per gram or particles per dollar. Additionally, we measure the mobility diameter, enabling the calculation of particle bulk densities, fractality, porosities, and more.
To introduce the potential of this measurement concept, we present the results of three commercially available iron red pigments, three carbon blacks, and a coated iron yellow pigment. First, some background information is provided on the relation between particle mass and diameter, collectively defining the particle structure, and then the experimental setup is briefly discussed.
Background: Mass Plus Diameter Equals Structure
The structure of a particle population is encoded in the relation between mass and diameter of the individual particles. The scaling relation between particle mass (m) and the particle diameter (d) can be expressed by Equation (1):
![]()
with a constant (k) and the fractal index (fi). While a fractal index of 3 indicates scaling of a solid object, a fractal index below 3 (and above 2, which would indicate plate-like scaling) signifies the scaling of an increasingly more porous material (see Figure A1). In the context of color pigments, the fractal index describes the branching of the aggregates itself and varies for every material. To visualize that, we examine the effective density, i.e., the density of a particle with mass m and diameter d assuming sphericity. Inserting Equation (1) for the diameter gives Equation (2).
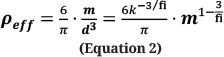
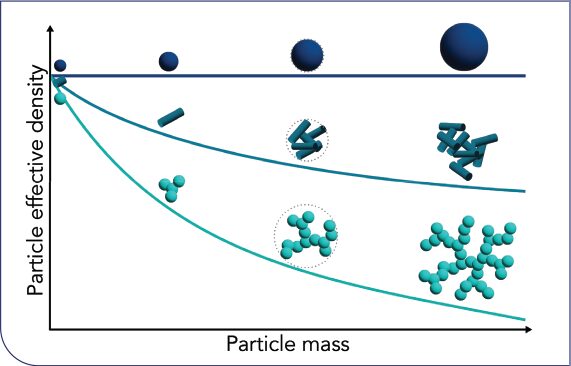
The scaling for three structurally different particle types is illustrated in Figure 1. Solid particles with a fractal index of 3 exhibit a constant effective density (in this special case, equal to the skeletal density). The effective densities of aggregated particles, here, as the example shows, columns and spheres (Figure 1), decreases with increasing mass, indicating a fractal index below 3. The stronger the decrease, the lower the fractal index and the higher the aggregation level of the particles.
FIGURE 1 Particle effective density as a function of particle mass for three structurally different particle types: Solid spheres (top), aggregated columns (middle), and aggregated spheres (bottom). Gray circles indicate a diameter estimate for visual guidance. Note: Same skeletal density is assumed. Particle mass axis is logarithmic.
The electrical mobility analysis is used to measure the geometric dimensions of a particle. Unlike other diameter estimates, the mobility diameter is not affected by the material density and refractive index. The mass is an intrinsic property of a particle and, unlike any equivalent diameter, it does not require any prior assumption and is independent of the measurement method. Therefore, the particle mass is well-suited to serve as a standard for the particle size.
Methods
We utilized a PowMaster system (femtoG AG, Switzerland), a combination of dedicated particle dispersion systems and the newly developed Mass & Mobility Aerosol Spectrometer (M2AS, Cambustion Ltd., UK), which enables the rapid measurement of size distributions for both absolute particle mass and a diameter (electrical mobility) within 5 to 15 minutes.
Powder analysis was initiated by an aerosolization of the powder material. Here we suspended 0.2 g of a pigment in 100 mL ultrapure water. The particles were deagglomerated by a finger-type ultrasound probe until an energy input of 100 J/ml was reached. Subsequently, the suspension was nebulized and the droplets were dried to retrieve the initial pigment particles. By producing small droplets and working with dilute suspensions, re-agglomeration during the drying process could be prevented.
Continue reading in the May-June digital issue of CoatingsTech
